DEAD ENDS : Part III : Justified lies

Here I am !
Bored of 2=1s aren't ya'll ? Here are some more of classic lies, told in the most decieving manner !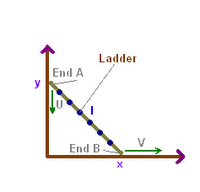


(1) *** classic *** ( Some PHYSICS for a change )
There in the figure, we have a ladder leaning against the brown wall. Its length is l & the two ends are labelled as A & B. End B is pulled in the positive direction of the x-axis with a constant speed V. The velocity of end A in the downward direction is U ( variable ). x,y are the respective coordinates of the two ends.

x² + y² = l²

differentiating w.r.t. time we get :

2.x.∂ x/ ∂t + 2.y. ∂ y/ ∂t = 0

2.x.∂ x/ ∂t + 2.y. ∂ y/ ∂t = 0
2.x.V = - 2.y.U(x)
U(x) = - x .V/ y

Now, when ladder falls completely, and becomes flat, then y = 0 & x = l.

To calculate the veocity of end A when ladder just becomes flat, we put the values in equation for U(x) getting :

U ( l ) = - l.V/0 = - ∞

So the velocity of end A becomes infinite when the ladder becomes flat ? !

(2)
We are all aware of the theorem of Mathematical Induction. However, none would have seen its misuse. Here is one such misuse which is horribly difficult to disproove !!!

Statement to be verified is :

S(n) : In any set of n people, all would have equal ages.

Now we proceed :

S(1) is true ( Since in a group(set) of 1 person, all have equal age. )

Let S(k) be true.

Now ;

In a group(set) of (k+1) people, we make all possible sets of k people. In all these possible set of n people, S(k) would be true (as per assumption) and hence all people in each of the sets would have equal members. Now since all such possible sets would have members of the same age, this is only possible if all the members in the (k+1) member be equally aged. Therefore All people in the set of (k+1) people have equal ages.

Hence S(1) is TRUE & S(k+1) is TRUE whenever S(k) is TRUE.

Hence prooved by mathematical induction , the TRUTH of statement S(n) for all n belonging to N.

Application of the above theorem for the set of BLOG MEMBERS "B" We conclude that All members of this blog are of equal age.
QED

(3) *** classic ***

ABCD is a square. BE = BC.
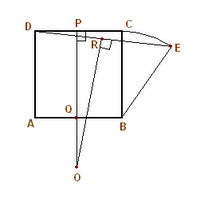
PQ bisects CD,AB.
OR is perp.bisect. of DE.
PQ, RO intersect at O.
∠ ABE is an OBTUSE ANGLE. ( clearly )

Δ ORD ≡ Δ ORE (SAS)
:. OD = OE

Δ OQA ≡ Δ OQB (SAS)
:. OA = OB & ∠ OAB = ∠ OBA

Δ OAD ≡ Δ OBE (SSS)
:. ∠ OAD = ∠ OBE
∠ ABE = ∠ OBE - ∠ OBA
= ∠ OAD -∠ OAB

But ∠ OAB - ∠ OAB
= 90 °

:. ∠ ABE = 90 °
However, we've assumed the angle to be obtuse. :. Every obtuse angle is a right angle. Similarly, It can be shown that every acute angle is a right angle.
QED

---

This is part III and I'll let ya'll know that 3's my lucky number. So hereby, I quit with this series. Not that the resources are over ! Infact they're endless. But today eve, I'm leaving for Delhi & I won't be able to be online so regularly. Though I'll surely stay in touch atleast twice a week !

A last message. I believe that us KVamPYs are special in some way. I also believe, that we can be a great strength when united ! So here's a request. Mayb you can't come online very often but do stay in touch by atleast going through the blog once a week !!!
This blog is for us KVamPYs, by us KVamPYs & of us KVamPYs.

So letz ROCK ... letz RULE !!!

& Ill borrow Rash's line...
SwItCh On Ur BuLbS !!!

~ Twishmay Shankar ~
( Twish ;-) )

span>