The Chaos Game

Here's about a lovely game I've been playing for the past week or so (it really screwed up my study schedule). It is just one of the pinnacles of the beauty of random processess. I hope you know I'm not talking about a computer game or sport.

I'll describe the basic process of the game now. It's very simple. Take a number of points (generally start with three, you can't do more without a program) on a piece of paper. Now supposing you've taken three (I'll assume you can all generalise it) points, considered vertices (A, B, C). Actually, these vertices need not be in ANY regular conformation. But again for aesthetic sense, consider them in an equilateral triangle. So you have three points in an equilateral triangle on a sheet of paper.

Now mark a point anywhere you like, inside the triangle, outside (even at infinity, but thats a wee bit impractical). This is your initial point, technically a seed. It really doesn't matter where its taken. Take a die (or create a random no. program). Assign two numbers to a vertex (if its a good die, which we assume it is, each no. has equally probability, so it doesn't at all matter). Suppose the following assigniations: A = (1,2) B = (3,4) C = (5,6). Roll the die, and mark your next point at the mid-point of your original point and the vertex indicated by the die. Roll the die again, and using the new pt. generate another pt. Continue doing it ad-infinitum (or till you go mad).
For example, let your initial pt be S. You roll a 4, then, mark X1 at the midpt of SB. Roll again, and get 3. X2 = midpt. of X1B. Roll:1. Mark X3 = midpt. X2A. Go on and on.

Honestly tell me what kind of figure would expect from such a random process. Some would say a filled triangle, and fewer a random figure that doesn't quite cover the entire triangle.

Time for some pictures eh?
Here is the plot for the above:
1. Plotted with just 10 points. No structure is inherent:

2. Plotted with 100 points. Some structure visible:

3.Plotted with 1000 points. Structure is glaringly obvious: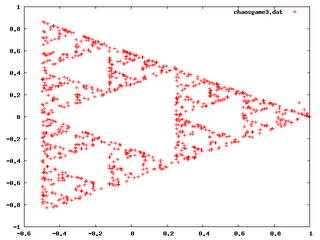

Just goes to show that the human intuition is extremely biased on its experiences. I've read two books about chaos, and a good portion goes in droning about how we've accustomed our minds to complex stuff can be achieved only by complex processes, and random processes bring out random results. The above figures tend to form the Serpienski Gasket, which is a figure that can easily be drawn through the process: Take a triangle, and exclude the triangle formed by joining the midpt of the sides. Do it for every single triangle you get. This is and example of a figure with INFINITE length but ZERO area. Another feature is that the figure is infinitely detailed, which means that it never lands onto the same spot, and no matter how deep you go into the figure, you will still see detail which is microscopic at that scale. It is also absolutely self-similar.

Either way, to extend the figures, we can take the points as 4,5,6, etc. (4 it comes out doesn't show anything, its and exception). We can also change the recursion to give:
X2 = (Vertex + X1)/R, where R is the ratio. Here we've taken R to be 2, and got the midpt. For different R, it doesn't exactly give us that.

So here are some more interesting pictures:

1) The same triangle, in much better detail (10^5 with a bettter plotter LabPlot, also freeware):
2) A skew triangle, just to show you the lack of need for regularity:
3) A hexagon with ratio 3. This is undoubtedly the most beautiful thing I've created (I don't draw very well):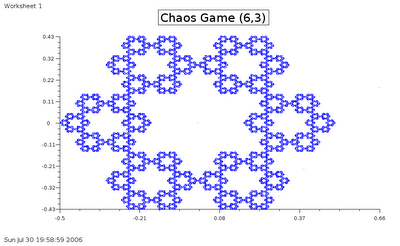
Just some more notes, the figure in the center is a Koch Curve, which to people who've read it is an amazing revalation, because of the amazing shape that it is. Just to tell you, take an equilateral triangle. Take the middle third of each side, and split it open into two parts to form an equilateral triangle with the side = 1/3 of the base length. __ becomes _/\_, with better ratios of course. Keep on doing this. It gives you finite area, but infinite length.

Ok. One last note: You really should try to experiment with this. You'll come across a lot of interesting, and semi-obvious realizations. For example, by changing the ratio R to 3 for the triangle, you'll get a similar triangle figure but each triangle will be a bit spaced. If you do the hexagon, with a ratio of 2 instead, you won't be able to make up much. Extrapolating ,the ratio gives how far apart they are, with too small a ratio, they'll overlap and you can't make out anything.
For further reference:
MathWorld: http://mathworld.wolfram.com/ChaosGame.html