DEAD ENDS : Part II : Burning Reality

Hi Again
As promised, here is PART II ...
Bewarethough !!! I'd certainly say this one is more wierd, more interesting but still a LIE which has been imposed wrongly upon reality :

(1)
Every1 here knows the pretty little Binomial thorem going as :

(a+b)ⁿ = aⁿ + n*b*a^n-1 + ... + n*b^n-1*a + bⁿ

Observing we find that leaving the first and last term, all other terms are a multiple of n.

For some wierd results, let us put n = 0 ;

LHS = (a+b)⁰ = 1

RHS = a⁰ + 0 ... + 0 + b⁰

= 1 + 0 ... 0 + 1

= 2

:. since LHS = RHS

2 = 1

QED

(2)

Consider the integral :

I = ∫ 1/x ∂x

Intigrating by parts ;

I = ∫ 1*1/x ∂x

= x*(1/x) - ∫ x*(-1/x²) ∂x

= 1 + ∫ 1/x ∂x

= 1 + I

:. 0 = 1

or, 2 = 1

QED

(3) *** CLASSIC ***

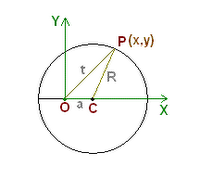
Have a look at the figure. O is the origin. C is the centre of the circle. P a variable point (x,y).

t = OP ; R = CP ; a = OC

The equation of the circle would be:

x² + y² -2*a*x + a² - R²

Now, t² = x² + y²

Also putting P(x,y) in circles equation we get :

t² - 2*a*x + R² - a² = 0

:. t² = 2*a*x + R² - a²

2*∂t/ ∂ x = 2*a

Now for the point with minimum distance , The above expression equals 0.

For that to be possible, a = 0, that is O and C are the same points !

Hence Whenever O is not the center of the circle, there is no point on the circle from which the distant of O is maximum or minimum.

QED

There is still more to come. Before thinking about the faults, appreciate the beauty of these propositions, how decievingly they proove the unproovable !

This in not the end.

~ Twish ~

---

NOTE : Those having difficulty typing math visit this link for keyboard codes :

http://www.planetburrito.com/tb/alt_codes.html