The Chaos Game
Here's about a lovely game I've been playing for the past week or so (it really screwed up my study schedule). It is just one of the pinnacles of the beauty of random processess. I hope you know I'm not talking about a computer game or sport.
I'll describe the basic process of the game now. It's very simple. Take a number of points (generally start with three, you can't do more without a program) on a piece of paper. Now supposing you've taken three (I'll assume you can all generalise it) points, considered vertices (A, B, C). Actually, these vertices need not be in ANY regular conformation. But again for aesthetic sense, consider them in an equilateral triangle. So you have three points in an equilateral triangle on a sheet of paper.
Now mark a point anywhere you like, inside the triangle, outside (even at infinity, but thats a wee bit impractical). This is your initial point, technically a seed. It really doesn't matter where its taken. Take a die (or create a random no. program). Assign two numbers to a vertex (if its a good die, which we assume it is, each no. has equally probability, so it doesn't at all matter). Suppose the following assigniations: A = (1,2) B = (3,4) C = (5,6). Roll the die, and mark your next point at the mid-point of your original point and the vertex indicated by the die. Roll the die again, and using the new pt. generate another pt. Continue doing it ad-infinitum (or till you go mad).
For example, let your initial pt be S. You roll a 4, then, mark X1 at the midpt of SB. Roll again, and get 3. X2 = midpt. of X1B. Roll:1. Mark X3 = midpt. X2A. Go on and on.
Honestly tell me what kind of figure would expect from such a random process. Some would say a filled triangle, and fewer a random figure that doesn't quite cover the entire triangle.
Time for some pictures eh?
Here is the plot for the above:
1. Plotted with just 10 points. No structure is inherent:
 3.Plotted with 1000 points. Structure is glaringly obvious:
3.Plotted with 1000 points. Structure is glaringly obvious: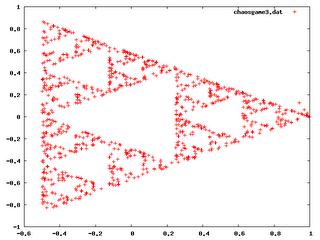
Just goes to show that the human intuition is extremely biased on its experiences. I've read two books about chaos, and a good portion goes in droning about how we've accustomed our minds to complex stuff can be achieved only by complex processes, and random processes bring out random results. The above figures tend to form the Serpienski Gasket, which is a figure that can easily be drawn through the process: Take a triangle, and exclude the triangle formed by joining the midpt of the sides. Do it for every single triangle you get. This is and example of a figure with INFINITE length but ZERO area. Another feature is that the figure is infinitely detailed, which means that it never lands onto the same spot, and no matter how deep you go into the figure, you will still see detail which is microscopic at that scale. It is also absolutely self-similar.
Either way, to extend the figures, we can take the points as 4,5,6, etc. (4 it comes out doesn't show anything, its and exception). We can also change the recursion to give:
X2 = (Vertex + X1)/R, where R is the ratio. Here we've taken R to be 2, and got the midpt. For different R, it doesn't exactly give us that.
So here are some more interesting pictures:
1) The same triangle, in much better detail (10^5 with a bettter plotter LabPlot, also freeware):
 2) A skew triangle, just to show you the lack of need for regularity:
2) A skew triangle, just to show you the lack of need for regularity: 3) A hexagon with ratio 3. This is undoubtedly the most beautiful thing I've created (I don't draw very well):
3) A hexagon with ratio 3. This is undoubtedly the most beautiful thing I've created (I don't draw very well):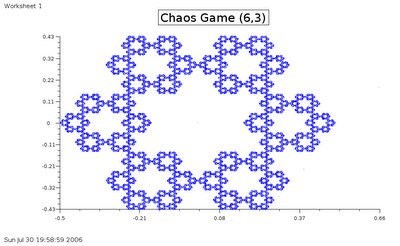 Just some more notes, the figure in the center is a Koch Curve, which to people who've read it is an amazing revalation, because of the amazing shape that it is. Just to tell you, take an equilateral triangle. Take the middle third of each side, and split it open into two parts to form an equilateral triangle with the side = 1/3 of the base length. __ becomes _/\_, with better ratios of course. Keep on doing this. It gives you finite area, but infinite length.
Just some more notes, the figure in the center is a Koch Curve, which to people who've read it is an amazing revalation, because of the amazing shape that it is. Just to tell you, take an equilateral triangle. Take the middle third of each side, and split it open into two parts to form an equilateral triangle with the side = 1/3 of the base length. __ becomes _/\_, with better ratios of course. Keep on doing this. It gives you finite area, but infinite length.Ok. One last note: You really should try to experiment with this. You'll come across a lot of interesting, and semi-obvious realizations. For example, by changing the ratio R to 3 for the triangle, you'll get a similar triangle figure but each triangle will be a bit spaced. If you do the hexagon, with a ratio of 2 instead, you won't be able to make up much. Extrapolating ,the ratio gives how far apart they are, with too small a ratio, they'll overlap and you can't make out anything.
For further reference:
MathWorld: http://mathworld.wolfram.com/ChaosGame.html



11 comments:
WHOAAA !!! Wow CHAOS !!!
Beg pardon for me only read the Header ! & got soo excited by the name of the topic itself to write this comment...
... Gr 8 job Arun ! More to comment wen I read the postie !!!
~ Twish ~
HEYYYYYYY ...
... I Think I have a REASON !!! Y the triangle in the first experiment somes out to be that particular triangle only that its not a triangle in the sense of a regular triangle. Its a famed entity which has the most beautiful property oif fractional dimensions !!! Strange > ? Or mayb you would have understood what I'm talking about is the fractal triangle we've obtained. Now did ne1 care to check out that the triangle in its dexterity exists not in 2-dimensions, 3-dimensions or ne other nice natural number labelled dimension which evolution has enabled us to visualize (Not that we can visualize much more than 3-D newayz... ). The remarkable thing is the trangle exists in "log 3" Dimensions. Thats more that strange isnt it ? For some it might be. I could write a whole post on this which I am curtailing from these times... So End with all this irrational dimension crapp... Newayz Take care guyz ... ~~~ !!!
TWISH
Hi!
Well, I couldn't read the post rite now (coz I'm reading it from the school) but I do like that u ppl are taking interest in the Chaos Game - we read about that in the Maths Lab - and fractals like Sirpinski's (dunno the spelling)....
Will read the post and comment soon...
:D
Yeah, twish, I know, its log 4 / log 3 = 1.261859507 dimension, but I don't see how that's gotta do with its formation. I think you know what kinda high I got when I somehow got the the equation for fractional dimension (I tried it for several figures and did it semi-empirically, but I have an explanation for it).
Perhaps my next post will cover that.
But till then, fractional dimensions aren't really all that counter-intuitive. This figure is not quite a 1-D figure, because it covers some space, but neither is it really a 2-D space because it doesn't really contain that space. So we consider it to be inbetweenie.
Hi!This is Rajat again. Not 1 of the geniuses like u but i also like thinking upto infinity.
This topic really needs more study as it is a diverse 1.
The Koch snowflake (or Koch star) is a mathematical curve, and one of the earliest fractal curves to have been described. It appeared in a 1904 paper entitled "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire" by the Swedish mathematician Helge von Koch. The less known Koch curve is the same as the snowflake, except it starts with a line segment instead of a equilateral triangle. The Koch curve is a special case of the de Rham curve.
One can imagine that it was created by starting with a line segment, then recursively altering each line segment as follows:
divide the line segment into three segments of equal length.
draw an equilateral triangle that has the middle segment from step 1 as its base.
remove the line segment that is the base of the triangle from step 2.
After doing this once the result should be a shape similar to the Star of David.
The Koch curve is in the limit approached as the above steps are followed over and over again.
The Koch curve has an infinite length because each time the steps above are performed on each line segment of the figure there are four times as many line segments, the length of each being one-third the length of the segments in the previous stage. Hence the total length increases by one third and thus the length at step n will be (4/3)n: the fractal dimension is log 4/log 3 ≈ 1.26, greater than the dimension of a line (1) but less than Peano's space-filling curve (2).
The Koch curve is continuous, but not differentiable anywhere.
The area of the Koch snowflake is 8/5 that of the initial triangle, so an infinite perimeter encloses a finite area.
Keep posting things like these.
Waitin to comment more.
If you calculate the area by basic principles, Koch Curve's area comes out to to be 32/21 of the actual area. 8/5 may be its approx.
Hi! Everyone
No post yet, waiting, ..waiting...waiting for more!
To correct you Mr Twishmay "sierpinski" triangle,-the right spelling, exists in log3/log2=1.55 dimensions.
Hey RAJAT
Whoever the hell u r. lol
I never spelt the triangles name! Though incase if I did & don't remember, I beg you an apology for us KVAMPYS have never cared about purist viewpoints & spellings ... the bottomline being the idea comes across.
Just rationalizing man, we all do it so allow me ... ;-) lolz.
Nice posting @ my site. U can call me Twish not "MR TWISHMAY" incase you care to lose ur sense of grown-up-manship. Hehe know that no such word (not even close) exists. Correct spellings on that ;-)
Just pissing u off heheh
TAKE CARE !
TWISH
I have to apologize, I didn't see your posts, since, the article was a bit down, ans I started to think it was dead. But as twish says, please post your info. Since you seem quite enthusiastic, please write an article too.
Post a Comment