 sequence if you please, was very dependant on the initial conditions. For practical purposes, an experimentalist prides himself if he can determine a physical quantity to the third decimal place. Here the absence of the fourth, fifth, and sixth decimals had erased all similarities to the original sequences within three-four cycles. What lorenz aptly demonstrated after this was that long term weather prediction was impossible. To do so he stripped down his system of equations for convection to their bare essence to three eqations.afterwards it was discovered that his equations mimicked a water-wheel- "At the top, water drips steadily into containers hanging on the wheel's rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other. " (James Gleick, Chaos - Making A New Science, pg. 29).This is a system of equations of the same family, or perhaps the same set that lorenz used, you can try plotting the behaviour of this system at home.
sequence if you please, was very dependant on the initial conditions. For practical purposes, an experimentalist prides himself if he can determine a physical quantity to the third decimal place. Here the absence of the fourth, fifth, and sixth decimals had erased all similarities to the original sequences within three-four cycles. What lorenz aptly demonstrated after this was that long term weather prediction was impossible. To do so he stripped down his system of equations for convection to their bare essence to three eqations.afterwards it was discovered that his equations mimicked a water-wheel- "At the top, water drips steadily into containers hanging on the wheel's rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other. " (James Gleick, Chaos - Making A New Science, pg. 29).This is a system of equations of the same family, or perhaps the same set that lorenz used, you can try plotting the behaviour of this system at home.
Whenever physicists encounter such a system they try to think of a quantity that is conserved, or in special cases, show predictable behaviour. Think of the simple harmonic equation D**2(x)=-w*x['**'=>raised to the power; here D**2=>d/dt(d/dt)]. in "phase space"- in which all possible states of the system is representable- this translates into a circle.Please note that lorenz was not aware of this terminology because this field of mathematics came in 1971. Say for turbulent flow in a cylindrical pipe, the elements of water that collide with the cylindrical wall, act as if it is attracted by the centre of the cross section of the pipe- THAT, thus, is the attractor in this system.Note that the elements that dont collide but are bound attractively to the surrounding elements also behave as if they are attracted, albiet by some different force law than inverse square. in lorenz' system, the attractor came out in the form of a double spiral.see picture.so although the momentary behaviour of the particle was seemingly random, in the long
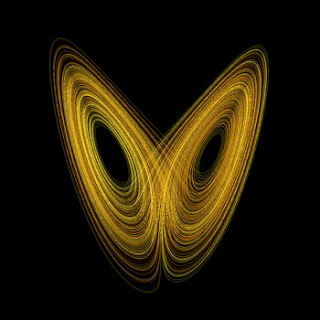 term, it was sketched out in the form of a ever-continuing, never intersecting double-spiral.sort of gives you insight into the butterfly effect- "The flapping of a single butterfly's wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month's time, a tornado that would have devastated the Indonesian coast doesn't happen. Or maybe one that wasn't going to happen, does. (Ian Stewart, Does God Play Dice? The Mathematics of Chaos, pg. 141)"
term, it was sketched out in the form of a ever-continuing, never intersecting double-spiral.sort of gives you insight into the butterfly effect- "The flapping of a single butterfly's wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month's time, a tornado that would have devastated the Indonesian coast doesn't happen. Or maybe one that wasn't going to happen, does. (Ian Stewart, Does God Play Dice? The Mathematics of Chaos, pg. 141)"The bottomline in this first phase of insight into chaotic systems was that certain systems behave too sensitively to their their initial conditions and that Lorenz' work established that long-term-weather forecasting was impossible. Now comes the sadder part of it, his paper was published in a Swiss Meterological Journal that lay in obscurity
 waiting to be rediscovered.
waiting to be rediscovered.The next story that defined birth of this new science was the work of Robert May, an ecologist in the 1970s. When one stands in the shoes of an ecologist and tries to model the population of, say fish in a pond, one inadvertedly realizes that the simplest model would be one in which there is unlimited food and the population of one year depends linearly on that of the previous year.i.e P(n+1)=a*P(n);P(n)=>population of the nth year.Now if you start taking into account the total food being constant,and the survival for existence, you arrive at :
With r between 3 and 3+(6)**.5[~3.45], the population oscillates between two values dependant on r.

Perhaps we got in too deep into this mathematical system than we intended to, but this isn't even starting to get technical.Robert May thus, showed how complex and beautifully simple systems like these can be at the same time.
The third story has to be that of Yorke who with Li proved that any one-dimensional system which exhibits a regular cycle of period three will also display regular cycles of every other length as well as completely chaotic orbits in 1975.Yorke's paper was named "Period three implies Chaos"- where he coined the term for use as we know it today.
For those attracted to abstract objects/theories of beauty, Smale's work on the mathematics of chaos was the first attempt that popularised the field of chaos to physics. His work can be, at its very basic simplification, be visualised by amazingly simple means. Consider a bar, bend it into a horseshoe shape and fold the whole thing overall again. the points that were initially distinctly apart originally, come together. The action of folding, however can represented by the difference equations operating on the variables. That's pretty much all a layman, like myself, can make of Smale's work.






.jpg)
.jpg)



